Требования к точности прицеливания

Вероятность F(R) попадания в круг радиуса R подчиняется закону Релея и может быть представлена в виде

 F(R) = 1- ехр-ln2(R /r)²                                                                                       

где R₅₀^к  – оптимальный по кучности радиус круга, охватывающий 50% дроби в осыпи, см;

r - срединная ошибка стрелка, см.

 

     Срединной ошибкой стрелка называется ошибка, при которой в половине выстрелов отклонение от цели меньше этой величины, а в половине выстрелов – больше этой величины.

     Из формулы 1 следует, что чем больше радиус круга R₅₀^к и чем меньше срединная ошибка r стрелка, тем больше вероятность попадания в цель. Такой вывод очевиден, однако интерес представляют не общие рассуждения, а величины этих вероятностей.

     На практике величина R всегда имеет конкретное значение. Либо это эквивалентный размер, поражающий  цель при стрельбе пулей, либо радиус окружности, внутри которого обеспечивается поражение цели при стрельбе дробью, так называемый радиус убойного круга R_уб. Таким образом,

                          F(R) = 1- ехр-ln2(R _уб/r)².                                             

     Но R_уб связан с радиусом R₅₀ соотношением  R_уб² = R₅₀²/ln2, где R₅₀ –радиус, охватывающий 50% всей дроби  в снаряде. Следовательно,

                          F(R) = 1- ехр-(R₅₀/r)².                                      

   Радиус R₅₀ зависит, прежде всего, от дистанции стрельбы и  сверловки ствола, а также от площади поражения дичи (цели) и числа дробин в снаряде.

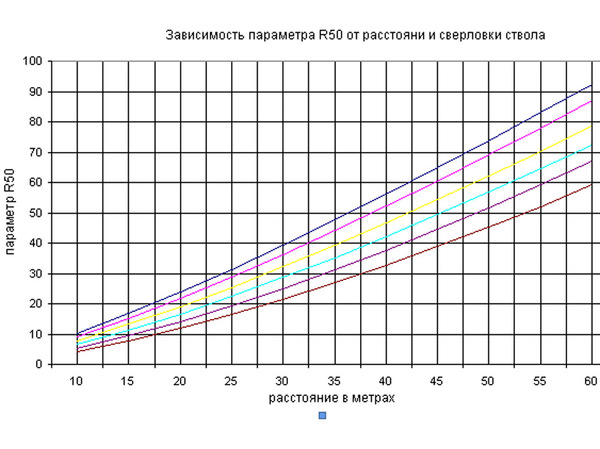
Зависимости радиуса R₅₀^к от расстояния и сверловки ствола представлены на рисунке, где сверху вниз расположены сверловки ствола: цилиндр, цилиндр с напором,  0,25 чока, 0,5 чока, 0,75 чока и полный чок.

 

Величина оптимального, то есть, максимально допустимого по кучности радиуса R₅₀^к  может быть вычислена по формуле

                            R₅₀^к = 0,142(S_дN₀)^0,5,                                                         

где  S_д – площадь дичи (цели), см²,

      N₀  - число дробин в снаряде.            

     А.А.Зернов в своей книге "Стрельба дробью охотничья и спортивная" писал, что у хорошего стрелка срединная ошибка прицеливания составляет 1% от дистанции, а у среднего стрелка - 1,5%. Позволю себе предположить, что очень хороший стрелок имеет ошибку 0,5%, а выдающийся - 0,3%. 

Кстати, такую величину отклонения от центра можно обнаружить и в статьях Ю.Константинова "Готовь патроны в марте" (РОГ №10 2007) и "Патрон и манера стрельбы" (РОГ №14 2007).

В первой статье он пишет: "… ошибка считается приемлемой и не повлечет промаха, если ее величина в пределах 20-30% от ширины осыпи". Поскольку R₅₀ составляет для  полного чока 0,9%, а для цилиндра до 1,6% от дистанции, то это и дает величину 0.3%.  Во второй статье   он называет цифру 10-15 см на расстоянии 35 м, что так же составляет 0,28-0,43% от дистанции.

Что же следует из этих формул и цифр? Подсчитаем, например, вероятности поражения цели стрелками, имеющими срединные ошибки 1% и 1,5% при стрельбе из цилиндра и полного чока на расстоянии, например, 35 м.

     Так  для полного чока согласно рисунку R₅₀^к = 27,5 см, а для цилиндра - R₅₀^к  = 48 см, то при ошибке стрелка 1% величина r равна 35 см, а при ошибке 1,5% - 52,5 см. Подставляя полученные цифры в формулу 1, получим:

- для стрелка с ошибкой 1% при стрельбе из полного чока вероятность поражения цели равна 46%, а

- для стрелка с ошибкой 1,5% при стрельбе из цилиндра вероятность поражения цели равна 57%.

     Из этого примера видно, что средний стрелок, умерив свои притязания на дальние выстрелы, стреляя из цилиндра, имеет больше шансов поразить цель, чем хороший стрелок, стреляющий из полного чока.

Поэтому при выборе ружья или сменных чоков надо соизмерять свои желания со своими возможностями. Между прочим, при этих условиях отличный стрелок имеет вероятность поражения цели 92%, а выдающийся стрелок – 99,9%, то есть 1 промах из 1000 выстрелов.

Таким образом, даже малые отклонения центра осыпи от цели весьма сильно влияют на результат выстрела. При стрельбе на предельных дистанциях площадь убойного круга (а не площадь осыпи!) катастрофически уменьшается, и очень скоро становится равной площади тушки дичи.

Тогда вероятность поразить 4 дробинами, например, тетерева на току на расстоянии 50 м (r = 50 см) дробью №5 с 32 г в снаряде (R₅₀ = 24,6 см) у хорошего стрелка равна 21%, то есть одно попадание из 5 выстрелов, а у среднего – 10%, то есть одно попадание из10 выстрелов.

     Интересно высказывание по этому поводу А.А.Зернова: «...то качество боя, за которым гонится большинство охотников – большая кучность – для большинства видов охоты только вредна». И еще. «Вообще можно сказать, что в настоящее время искусство сверловки стволов обогнало искусство стрелков». Это было опубликовано в 1934 г. Сейчас ружья стали ещё лучше, но все ли охотники их достойны?

     Воспользуюсь случаем, чтобы обратить внимание на фривольное обращениями некоторых авторов с величинами дистанций таких как, например, 35 и 40 м, как будь-то 35 и 40 это, как бы, одно и тоже.

Каждый метр увеличения расстояния до цели вносит свой негативный вклад в результат выстрела. Так плотность осыпи дроби на 40 м по отношению к 35 м у цилиндра уменьшается на 71%, а у полного чока - на 26%. При скорости полета цели 20 м/с, через  каждые   0,25 с цель буде удаляться на 5 м. Так что самая, казалось бы, простая для стрельбы траектория полета цели на самом деле требует расторопности.  

 В своё время мы с двоюродным братом мечтали приобрести ружья с двумя парами стволов. Наконец, ему удалось приобрести довольно потрёпанное импортное ружье, у которого были длинные стволы с сильными чоками и короткие – цилиндр с напором и слабый чок.

Первое, на что мы обратили внимание: короткие стволы были довольно сильно корродированны, а стволы с сильными чоками были почти новые. Такими остаются они и до сих пор. Надеюсь, теперь вам ясно почему. Как говорили старые охотники: «Кучное ружьё малодобычливо!».

     Ну, вот наступило и время, и место, что бы решить, наконец, проблему пресловутых дальних выстрелов.

  Представим себе, что на всех дистанциях скорость дроби постоянна и равна 200 м/с, убойный круг также остается постоянным, а ошибка стрелка равна 1% от дистанции. При таких условиях можно стрелять аж до 100 м, но что мы получим при этом? Найдем вероятность поражения гуся на этом расстоянии.

  При массе гуся 4 кг кинетическая энергия 4 дробинок для его поражения должна составлять 36 Дж, то есть 9 Дж на одну дробинку. Следовательно, масса одной дробинки должна быть 0,45 г, что соответствует дроби №0 при 79 штук в снаряде 36 г. Радиус R₅₀ = 24,6 см. 

Отклонение центра попадания от линии прицеливания на 1% от расстояния 100 м составляет 100 см. По формуле 1вероятность поражения равна 6%, то есть 1 гусь из 17 выстрелов.

На одного гуся потребуется израсходовать до 600 г дроби.  При этом надо иметь в виду, что дробь будет лететь 0,5 с и снизится за это время на 1,2 м. А тут еще и ветер может подуть ... Как видим, даже такое идеальное ружьё вряд ли может быть использовано при стрельбе по неподвижной цели.

 Напоминаю, что расчет вёлся для хорошего стрелка. Для среднего стрелка результаты будут менее утешительными. Стрельба одновременно из обоих стволов из ружья J.E.T Canardous снарядами дроби по 52 г в каждом увеличивает дальность стрельбы всего на 5 м, правда, вероятность поражения равна 32% - 1 гусь из трех выстрелов, а количество дроби сокращается до 300 грамм. Ради одного гуся мы за ценой не постоим, не правда ли?  У рыбаков это звучит так: «Килограмм червей на килограмм рыбы».

Возможно, некоторым читателям эти цифры окажутся неправдоподобными, а автор – не в себе. Тогда обратимся к строкам статьи «Оружейные припасы для охоты на гуся» Анатолия Азарова – члена ассоциации «Арсенал» (журнал «Арсенал Охотника» №4 апрель 2004): «Недавно мой приятель пристреливал свои патроны на гуся. Дробь 0000. Результаты таковы: на 35 м в круге диаметром 760 мм – 31 пробоина, на 50 -12 попаданий, на 70 метров – круге 2 дробины … Пыл его сразу угас».

Вы скажете, что его  приятель просто не умеет снаряжать патроны. Напрасно. К сожалению, в статье не было указано, из какого ствола велась стрельбы, и какова была навеска дроби. Поэтому я пересчитал вышеуказанные цифры при стрельбе из ствола 0,5 полного чока и 32 г дроби (N₀ = 43).

И вот что получилось: 35 м – 29 дробин, 50 м – 15 дробин, 70 м – 7 дробин. Как видим, результаты довольно близкие, а на 70 м при расчёте получилось на 5 дробин больше, но это в круге, площадь которого  в 12 раз больше площади тушки гуся!

     И ещё. Прежде чем посягать на дальние выстрелы, необходимо каждому стрелку знать свою срединную ошибку. Для её определения совсем необязательно производить выстрелы. Для этого потребуется либо фонарь с узким пучком света, либо лазерная указка, устанавливаемая на ружье и включаемая при нажатии на спусковой крючок.

Появились сведения и о патронах-фонарях, вставляемых в ствол и включаемых при ударе бойка. Произведя несколько десятков «выстрелов» по целям, установленных на известном расстоянии, и, отмечая каждый раз отклонение линии прицеливания от центра мишени, можно определить среднее значение всех отклонений. Однако при таком способе необходим помощник, что не всегда возможно.

Для этой цели подошли бы вкладные стволики, стреляющие одной дробинкой или шариком  диаметром 4,5 мм. Зарядом при этом мог бы служить капсюль «Жевело» или строительный патрон.